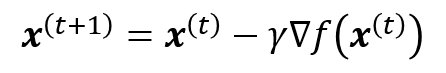Deep Learning - Gradient and Exploding Gradient

Gradient 梯度

Gradient 是偏導數的向量
一個多變量函數的偏倒數向量
對於單變數函數，梯度就是斜率

又稱為 Delta rule

沿著 gradient 往下找，找到局部最小值

梯度下降法是一種不斷去更新參數找解的方法
先隨機產生一組初始參數的解，然後根據這組隨機產生的解開始算此解的梯度方向大小，然後將這個解去減去梯度方向

透過 learning rate η 來更新 w

是 Error Fuction E(w) 最陡的 descent

因為，所以 w 會越更新越小
透過 decrease w 去 minimize error ，因此會找到線段往左下的局部最小值

因為，所以 w 會越更新越大
透過 increase w 去 minimize error ，因此會找到線段往右下的局部最小值

One weight without bias:

$ŷ$

: 輸出值
$ŷ$ : 預測值

if 且只有一組 training example

The gradient of E

$ŷ$
$ŷ$

: 輸出值
$ŷ$ : 預測值

$ŷ$
$ŷ$

: 輸出值
$ŷ$ : 預測值

比較不常用
沿著 gradient 往上找，找到局部最大值

梯度爆炸原因:
模型更新使用反向傳播法，每傳遞一層會乘上一大堆東西，當某一層的參數特別大，一路傳下去就會越瘋狂放大，這個往上遞增趨勢非常快速，導致梯度爆炸

會導致越靠近輸入的那幾層更新速度非常快，使模型輸出結果瘋狂震盪

透過正規化 L1 regularization、L2 regularization 可以很好的處理梯度爆炸

梯度消失原因:
模型更新使用反向傳播法，每傳遞一層會乘上一大堆東西，當某一層的參數特別小，一路傳下去就會越乘越小，這個往下遞減趨勢非常快速，導致梯度消失

當誤差資訊因此而消失時，無法有效更新所有模型參數

ReLU activation function 遇到梯度消失的影響會比較小

long short-term memory (LSTM) 網路，因其 residual neural network 的 skip connection 特性，使其可以訓練更深的神經網路