Machine Learning - Linear Regression & Logistic Regression


Classification vs. Regression
Classification:預測的 y 是不連續的值,輸出的 label 是分類 categorical
例如:是否換手機、喜歡什麼顏色
Regression:預測的 y 是連續的值,輸出的 label 是數值 numeric
例如:預測房屋價格、預測股價、預測體重
Regression 必回傳數值
Regression
Regression 必回傳數值
1. Linear Regression
屬於 Supervised Learning
透過建立輸出是一個數值,輸入是多個數值這樣的關係的模型的線性方法
若輸入只有一個 x,找到的就是一條直線 ŷ = b + wx
若輸入有許多個 x,找到的就是一個超平面 hyperplane ŷ = b + w1x1+ w2x2+ w3x3+ w4x
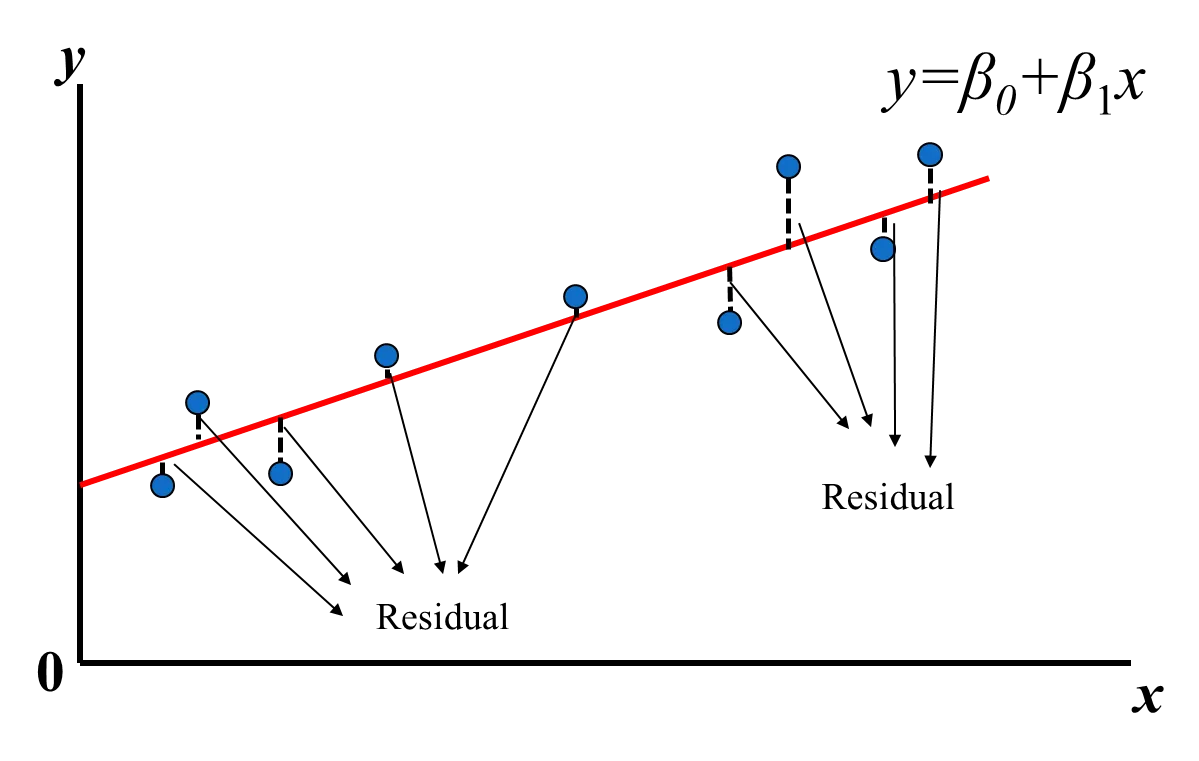
回歸分析是在找 y = β0 + β1x 中的 β0 與 β1
讓目標函數與損失函數 loss function 找到的模型最終 error 越小越好
找法為:
帶入資料 (xi, yi), i = 1, …, n,會產生
ŷi = β0 + β1xi,i = 1, …, n
ŷi: 為預估出的值,和真實資料會有誤差 (error),因此可得下式:
εi = yi — ŷi
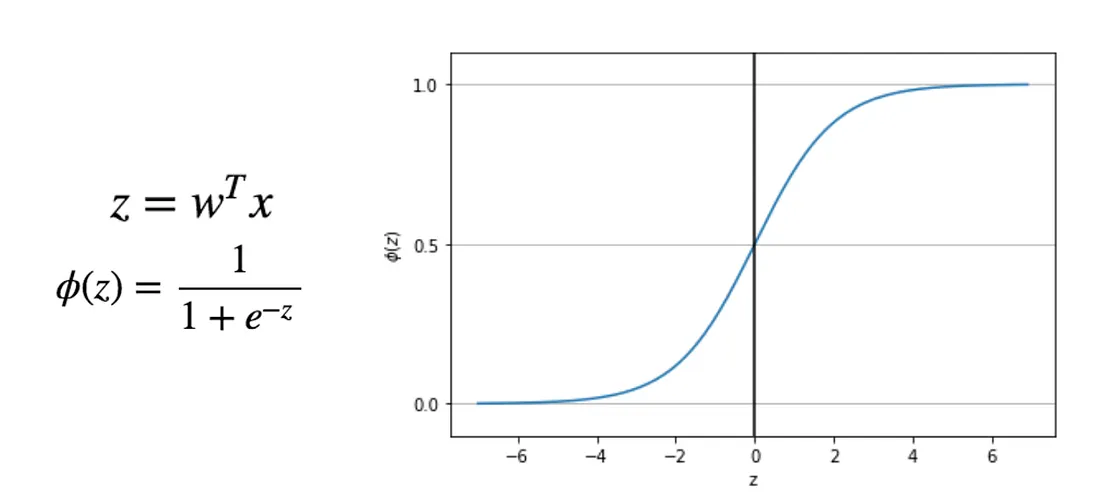
2. Logistic Regression
不是使用 squared loss 最小化損失函數,而是根據模型最大化訓練集的可能性
n = wTx + b = w∙x + b (內積)= w1x1 + w2x1 + b
Linear Regresson VS Logistic Regression
| Linear Regresson | Logistic Regression | |
|---|---|---|
| 輸出 | 連續的數值 | 機率,表示某個類別的機率 |
| 用途 | 預測連續型變量的值 | 處理二元分類問題 |
Reference
- Hundred-Page Machine learning Book by A. Burkov
- 黃貞瑛老師的機器學習課程
- 機器學習-支撐向量機(support vector machine, SVM)詳細推導
- [資料分析&機器學習] 第3.5講 : 決策樹(Decision Tree)以及隨機森林(Random Forest)介紹