
Pattern Recognition - An improved handwritten Chinese character recognition system using support vector machine

雖然是 2005 年的論文,但因為上課需要報告所以還是學習了一下
順便附上我們做的簡報:
Introduction
Abstract
本文描述了幾種改進中文文字識別系統的技術。透過增強非線性正規化、特徵提取,在具有數千個類別的大資料集上調整 support vector machine 的參數,來提高整個系統的性能。
手寫中文文字具有複雜的結構和形狀變化,還存在許多相似的模式,導致基於像素值的方法表現不佳,因此會透過預處理步驟(例如:形狀正規化和特徵提取),來對資料進行預先處理。
使用非線性的數學變換(如對數、指數、平方根等)來調整數據。這些變換可以根據數據的分佈特性來選擇,以達到更好的均勻化效果
用統計分類最小化的原則來估計一個分類的 hyperplane 超平面
透過找到一個 Decision Boundary 決策邊界來讓兩類之間的邊界最大化,使其可以完美區隔開
不一定是直線,有可能是曲線,不同的演算法都是在不同的假設或是條件下去找那條分類的線
Nonlinear normalization
非線性正規化 Nonlinear normalization
Nonlinear normalization 是用於糾正非線性形狀變化和均勻化二維線密度,使空間能夠更有效地利用,並穩定特徵採樣點以進行 pattern 的匹配,
但此方法僅對二維圖像進行操作,非線性正規化可能會產生許多鋸齒狀,會對特徵提取有很大的影響,很難在不破壞筆劃信息的情況下將其平滑。
指在二維空間中,沿著某些線條分佈的數據點的密度。例如,圖像中表示某些特徵的邊緣。
平滑(smoothing)是指通過某些算法或技術來減少這些鋸齒狀的邊緣,使得數據或圖像變得更加連續和柔和
LVQ & MQDF
學習向量量化 Learning vector quantization, LVQ
修改二次判別函數 (Modified quadratic discriminant function, MQDF)
許多優秀的分類器如多層感知器,由於建模的複雜性和「局部最小值問題」,不能直接應用於具有數千個類別的手寫中文字元識別,
現在手寫中文字元的兩種主要分類方法為:
- 透過 LVQ 生成一些代表性的參考模式作為模板
- 修改二次判別函數 (Modified quadratic discriminant function, MQDF)
LVQ 的決策邊界 (Decision Boundary)是成對的超平面 (hyperplane),當實際類別邊界是非線性的時,會產生較大的偏差;
MQDF 假設每個類別中的資料是高斯分佈,用最大似然(maximal likelihood approach)方法生成每個類別的密度模型,然後使用貝葉斯決策規則(Bayesian decision rule)進行分類,
因為在沒有足夠先驗知識的情況下,類別密度的估計通常是一個困難問題,
本文的目的是通過使用改進的非線性正規化方法和支持向量機(SVM)來提高手寫中文字符的識別精度,
非線性正規化應用於灰度圖像,可以去除鋸齒狀,同時保留邊緣信息。
SVM 通常應用於類別較少的分類問題,如手寫數字識別
用於分類任務,通過學習代表每個類別的原型向量,根據訓練樣本是否被正確分類,調整這個原型向量:
如果分類正確,將原型向量向訓練樣本移動。如果分類錯誤,將原型向量遠離訓練樣本移動。重複上述過程直到收斂進行分類
LVQ 的決策邊界是由一組超平面組成的。如果數據的實際分類邊界是彎曲的或非線性的,LVQ 可能會產生較大的誤差,因為它的邊界是直的
修正後的協方差矩陣,構建二次判別函數,用於評估樣本點屬於各個類別的可能性。對每個類別的協方差矩陣進行特徵值分解。保留主要的特徵值和特徵向量,並用平均值替代較小的特徵值
最大相似(maximal likelihood approach)方法
是一種統計方法,用於估計模型參數,使得在給定數據下,模型生成這些數據的可能性最大
用於在不確定性條件下做出最優決策。其核心思想是利用先驗知識和觀測數據來計算後驗概率,然後基於最小化期望損失(或最大化期望效用)來進行決策
Improved nonlinear normalization
對於數字圖像,當用離散網格表示具有尖銳邊緣和平滑曲線的細節時會發生混疊 (aliasing)。
混疊就是:當一條具有尖銳不連續性的直線顯示在電腦屏幕上時,會看到的鋸齒狀就是混疊引起的,但可以透過在高於最終所需的分辨準確率下取樣連續圖像,接著應用抗混疊濾波器 (用來限制訊號的頻寬用) 來去除,然後再降採樣到所需分辨率來最小化。
為了在非線性正規化後有效去除鋸齒狀,我們在二維圖像上確定取樣點的位置並生成灰度圖像,
因為噪聲過濾和邊緣平滑在灰度圖像上比起在二維圖像上會更容易,
本文應用的非線性正規化結構的示意圖:
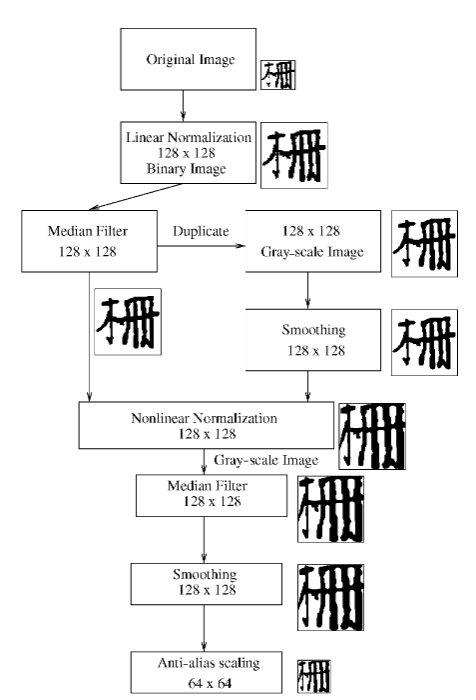
非線性正規化應用於二維圖像以計算取樣點的位置,好生成灰度圖像,x 和 y 軸上的特徵投影函數定義為公式如下:
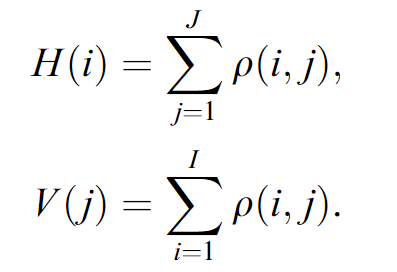
令
Forward function
將輸入圖像中的位置 (i,j) 映射到正規化圖像中的位置 (m,n) 由以下公式導出:
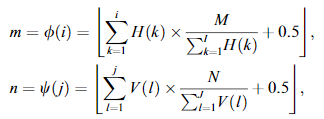
其中
而以下公式說明了輸出圖像的像素值來自於原始圖像中的一個像素:
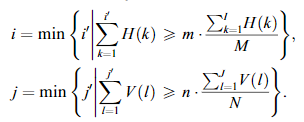
由於輸入和輸出圖像的離散性,輸入圖像的許多取樣點可以映射到輸出圖像中的同一點,而論文中考慮這些輸入取樣點的所有特徵。
定義集合
為了確保正規化圖像中所有位置的像素值,需要進行反向映射,下圖顯示了 m 的反向映射:
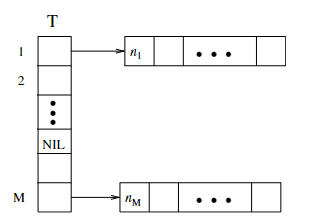
元素
數組的起始地址的指針。
即沒有輸入索引
為了計算正規化圖像中的所有像素值,T 中的每個元素必須是一個非空指針,當 T 中的一個元素為空時,就將最近的非空元素分配給它。
這樣可以確定索引 n 的反向映射,正規化圖像中的每個像素都可以有其在輸入灰度圖像中的對應像素。
如果輸入圖像中的多個像素映射到正規化圖像中的同一像素,就把這些源像素中的最大值分配給目標像素,這樣的操作可以減少鋸齒狀的影響。
前述的方法解決了混疊的問題,使用不同的方法的圖像如下:

(A) 原始圖像
(B) 未改進 nonlinear normalization 前的圖像,在外圍區域的筆畫會變形
(C) 使用改進 nonlinear normalization 的圖像
Feature extraction
大多數中文字由筆劃組成,所以可以將手寫中文字分解為多個方向的子圖像,並進行各方向分析,
本論文的正規化方法會生成灰階圖,基於圖像梯度計算特徵提取的過程如下:
- 將灰階正規化圖像標準化,使其均值和最大值分別為
0和1.0 - 將
64×64的正規化圖像置於80×80的框內,有效利用四個邊緣區域的
資訊 - 應用邊緣運算符計算圖像梯度的強度和方向
- 將圖像劃分為
9×9個大小為16×16的子區域,每個子區域與相鄰子區
域重疊8個 pixel。
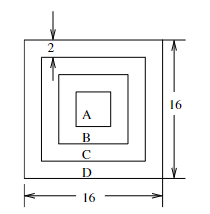
- 每個子區域分為四部分:A、B、C 和 D。
A 是中心的 4×4 區域。
B 是除去 A 區域的 8×8 區域。
C 是除去 B 區域的 12×12 區域。
D 是除去 C 區域的 16×16 區域。
- 累積每個區域 A、B、C、D 中
32個向量化方向的梯度強度。為了減少位置變化的副作用,使用一維掩碼(4, 3, 2, 1)對每個方向的累積梯度強度進行降採樣,結果會得到一個大小32的特徵向量,也就是[32 x 4] x [4 x 1] = [32 x 1]。 - 接著再使用一維掩碼
(1, 4, 6, 4, 1)進行降採樣,將方向分辨率從32降至16,作法為把32分成五個掩碼窗口,窗口一有1個元素、窗口二有4個元素 … 窗口五有1個元素,總共大小1 + 6 + 4 + 4 + 1 = 16的向量。 - 最後生成一個大小為
1296(9個水平,9個垂直和16個方向分辨率,9x9x16 = 1296)的特徵向量。 - 對特徵向量的每個分量應用變量變換
,使每個分量的分佈接近常態分佈。 - 將特徵向量按一個常數因子進行縮放,使特徵分量的值範圍在
0到1.0之間。
Parameter selection for support vector machine
給定訓練向量
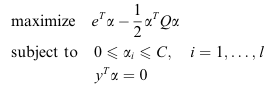
其中 1 的向量,
convex quadratic optimization problem(凸二次規劃問題):
凸二次規劃問題(convex quadratic optimization problem)是指一類凸優化問題,其目標函數是一個凸二次函數,約束條件可以是線性的或者是凸的
半定核矩陣(semidefinite kernel matrix):
當我們在機器學習中處理數據時,有時需要量化數據樣本之間的相似度或者內在關係。半定核矩陣是一種特殊類型的核矩陣,任何非零向量與該矩陣相乘後的結果都是非負的,可以幫助我們處理非線性問題,就像論文中 SVM 和 kernel 主成分分析中,通過使用半定核矩陣確保所得到的結果是合理的
透過選擇一個包含較少類別的訓練子集和驗證集,使選擇的這個過程成本較低,且這些類別的 pattern 相似或容易被錯誤分類,方法如下:
- 根據類別對訓練數據進行分組
- 將每個類別的訓練數據分為兩部分:75%用於訓練,其餘用於驗證
- 對每個類別使用具有低計算成本的判別函數,例如:歐幾里得判別函數
,( 是類別 的均值向量, 是類別的數量) - 在驗證集上評估判別函數的性能,並計算混淆矩陣 (confusion matrix),其定義為:
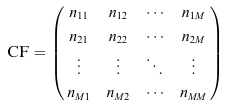
其中每一行
- 根據每個類別計算錯誤分類的樣本數量,公式如下:
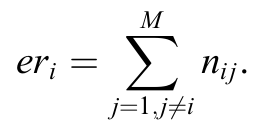
- 對
按降序排列,獲取前 ( 遠小於 ) 的選擇下標 - 根據混淆矩陣找到可以分類到類別集合
𝑺$,如下:
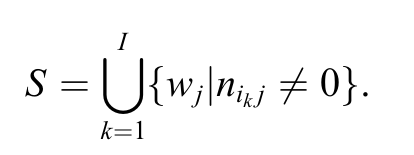
- 從類別集合
中選擇訓練集和交叉驗證集,以調整 SVM 的 和 kernel function
獲得
用於將輸入樣本分類到不同類別或類別之間的一種函數,接受一個或多個輸入特徵,並返回一個類別標籤或類別概率
基於歐幾里得距離的概念,即兩個點之間的直線距離,對於給定的輸入樣本,歐幾里得判別函數會計算該樣本與每個類別的代表點(通常是該類別的中心)之間的歐幾里得距離
Experiments
論文的資料集使用的是由日本電氣技術實驗室創建的 ETL9B 資料集,
我們實際上網找到的開源數據庫連結如下,其中 ETL9B 的數據庫字元如下:

http://etlcdb.db.aist.go.jp/specification-of-etl-9
該數據庫包含 3036 類別,每類有 200 個樣本
所有樣本都是大小為 64(寬)x 63(高)的二維圖像
該數據庫中的樣本被分為五組(A 到 E),每組每類有 40 個文字
在論文的實驗中,A 組到 D 組用於訓練,E 組用於測試
所以訓練集和測試集的大小分別為 485,760 和 121,440 張圖片
對於前面提到的 SVM,論文的建構方法為使用
一對多的方法構建 3036 個 classifier
每個 classifier 都會將其中一個指定類別與其餘類別分開
論文使用的分類決策:選擇 classifier 輸出值最大的類別
Pattern 使用 3x3 遮罩 (mask) 進行平滑處理,中心元素設為
特徵提取中的常數因子設置為 0.05,在判別分析後,1296 維特徵向量減少到 392 維
分類器接收到一個新的輸入樣本時,它會根據該樣本的特徵值和模型的參數,進行一系列的計算和判斷,最終將該樣本分類到某一個類別中
ETL9B 有 3036 個類別,為了減少計算成本並加快分類速度,需要使用預分類器來獲得較高的累計識別率,這樣只有少數幾個選定的候選者包含真實的類別標籤
論文使用的是應用歐幾里得判別函數來選擇 20 個候選者(在即便是第 20 名的候選者,累計識別準確率也有 99.92%)使用具有 RBF 核的 SVM 作為主要 classifier,再從這些候選者中做出最終決策
RBF 核的定義為: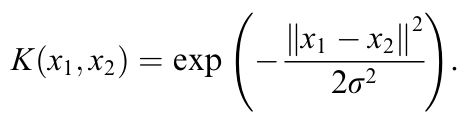
作用是將原始特徵空間映射到更高維的特徵空間,從而使得非線性問題可以在高維空間中被線性分類
再從從前面 Parameter selection for support vector machine 中提出的方法來確定
論文中使用歐幾里得判別函數並將參數 20,集合 144
而論文的實驗結果,當 0.8 的時候,驗證集達到最好結果
在訓練集上,由於每個類別僅有 160 個樣本,這樣樣本數太少,所以要增加訓練樣本的數量,論文中提到透過將每個訓練圖像在四個方向(左、右、下、上)各移動一個像素,來做資料擴充
移位後的訓練集大小為 2,428,000,下表顯示了 SVM 在 ETL9B 的識別準確率,
SVMa 是在原始資料集的訓練結果,SVMb 是在位移資料集的訓練結果
從 Substitution error 可以看出 SVMb 只略微提高了性能,並不是非常有效
但在論文中提到直到改成使用二次判別函數作為主要 classifier 時,才在 Substitution error 取得了 0.95 的替代錯誤率

是一種用於對多類別問題進行分類的方法。它屬於線性判別函數的一種擴展,通常用於將樣本映射到多個類別中的一個。這種方法的名稱源於其決策邊界(decision boundary)是二次曲線的形式。
下圖表示了 ETL 測試集的錯誤分類
箭頭左邊是該字元的原始標籤
右邊是被錯誤分類的字元標籤

Conclusion
本論文的貢獻為:提出了一種非線性正規化方案的方法,
以 ETL9B 手寫漢字做為資料集,構建了一個高性能 SVM
這種新方法具有消除正規化圖像周邊區域的鋸齒效應和筆畫變形的優勢,
適用於生成包含少量類別的資料集,
以便 SVM 處理具有數千類別的大型數據集上的大規模分類問題。